無料ダウンロード x y/2=4 x/3 2y=5 by substitution method 100224-X y/2 4 x/3 2y 5 substitution method

  Solve the system of equation by using substitution method 2x5y=22 y=x5 6 Solve the system of equation by using substitution method y=2x1 5y6x=13 7Solve by substitution 8x2y=44 9x2y=58 8 Solve by using substitution x4=y 5x5y= 9 Solve by substitution method x5y=15 2x10y=16 10 Traffic signs are regulatedAnswer (1 of 2) If x y = 4, Then y = 4 x if y = 4 x Then 2x (4 x) = 5 by substituting y's value in terms of x into the equation 2x (4 x) = 5 2x 4 x = 5 x = 3 If you use the first equation, x y = 4 Then substituting x gives you 3 y = 4 Which means y = 1 So x = 3 an So, now we substitute 3 – 4y for the value of x in equation A Equation A is 3x 2y = 4 3x 2y = 4 3(3 – 4y) 2y = 4 Step 4 Perform the multiplication 3(3 – 4y) 2y = 4 (3 × 3) – (3 × 4y) 2y = 4 9 – 12y 2y = 4 Step 5 Perform inverse operations to solve for y 9 – 12y 2y = 4 9 – 9 – 12y 2y = 4 – 9

6 3 Substitution Method Simultaneous Linear Equations Siyavula

X y/2 4 x/3 2y 5 substitution method

X y/2 4 x/3 2y 5 substitution method-Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you X/22y/3=1 and xy/3=3 solve by elimination method Get the answers you need, now!

Solve X Y 7 And 3x 2y 11

 Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 22(x y) = 2 × 52x 2y = 10 Solving (3) and (2) by Elimination–5y = –6 5y = 6 y = 𝟔/𝟓Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 − 6)/5 x = 𝟏𝟗/𝟓Hence, xSolve each pair of equation by using the substitution method 0 2 x 0 3 y = 1 3 0 4 x 0 5 y = 2 3 Medium View solution > Solve the following pair of linear equation by the substituting method 3 xAnswer to Solve the system by the method of substitution a) y = 2x^2 y = x^4 2x^3 b) x^2 y^2 = 169 3x 2y = 39 By signing up, for Teachers for Schools for Working Scholars

Question Solve the system using the substitution method x 2y = 6 3x 2y = 2 This is what I did 3x 2y = 2 x = 2y 3 _____ (2y 3) 2y = 6 = 2y 2y = 3 _____ y= 3 _____ x = 2y 3 x= 2 (3) 3 x = 9 I checked my solution and it was wrong I don't know where I messed up Answer by jerryguo41(197) (Show Source)Solve for y for the first equation Subtract from both sides Divide both sides by 4 Which breaks down and reduces to Now we've fully isolated y Since y equals we can substitute the expression into y of the 2nd equation This will eliminate y so we can solve for x Replace y with Since this eliminates y, we can now solve for x Distribute 4 to MultiplyCancel the common factor Divide y y by 1 1 Divide 3 3 by 3 3 Replace all occurrences of y y with 1 1 in each equation Tap for more steps Replace all occurrences of y y in x = y x = y with 1 1 Remove parentheses The solution to the system is the

Answer x = 4 x = 4 and y = − 1 y = − 1 Equivalently, the solution is ( 4, − 1) ( 4, − 1) Remember, a solution to a system of equations must be a solution to each of the equations within the system The ordered pair (4,−1) ( 4, − 1) does work for both equations, so you know that it Click here 👆 to get an answer to your question ️ 7x15y =2,x2y=3 find the value of x and y by substitution method RamanRandhawa RamanRandhawa The Questions and Answers of 04x 03y=17 07x02y=08 7(y 3)2(X 2)=14 4(y2) 3(x3)=2 X y/2=4 X/3 2y=5 solve this in two min From substitution, elimination,and cross multiplication method?

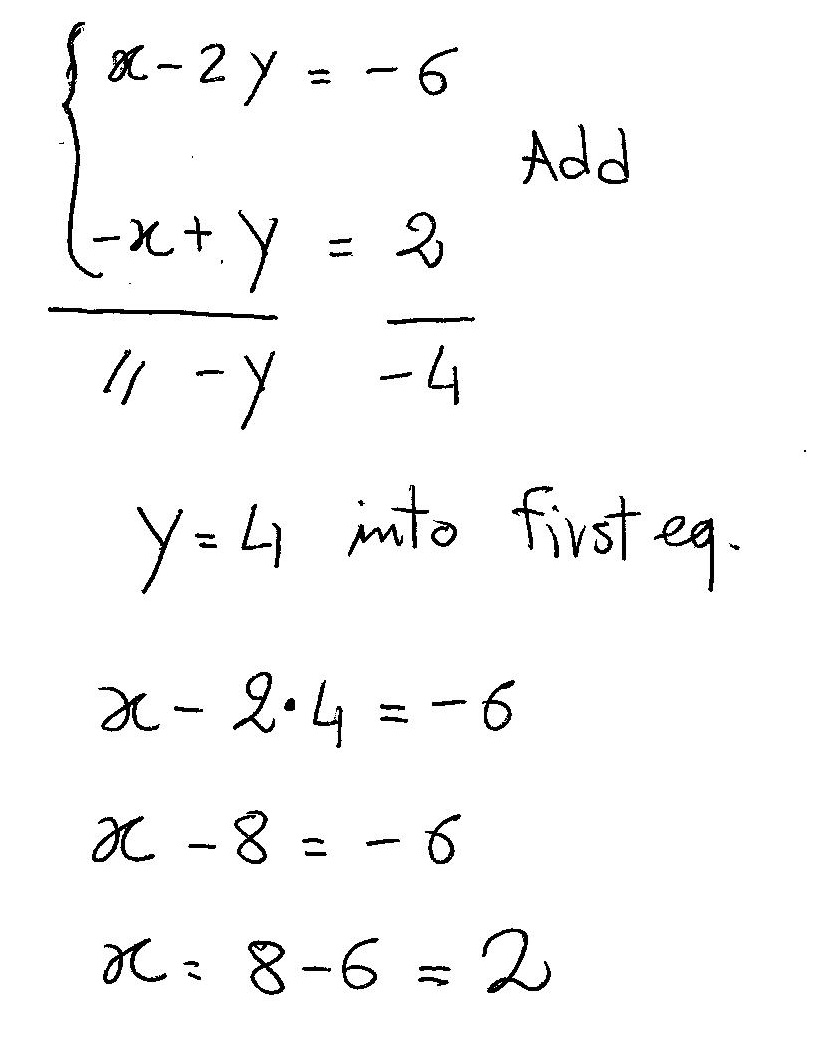
How Do You Solve X 2y 6 And X Y 2 Socratic

Revision 1 Simultaneous Linear Equations In Two Unknowns A Pair

 Explanation 5x y = 1 Eqn (1) y = 1 −5x 3x 2y = 2 Eqn (2) Substituting value of y in second equation in terms of x, 3x (2 ⋅ (1 −5x) = 2 3x 2 −10x = 2 −7x = 2 −2 = 0 or x = 0 Substituting value of x in Equation (1),Solve system of equations unsing substitution method stepbystep \square!(x, y) = (2, 3) Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here If you have any feedback about our math content, please mail us

2

3x 2y 5 2 And 1 3 3y 4 3 Problem Set 1 Q5 3 Linear Equation In Two Variables Youtube

Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10 NCERT Solutions for Class 10 Maths Chapter 3 Exercise 34 Question 1 Summary On solving the pair of equations by the elimination method and the substitution method we get x, y as (i) x y = 5 and 2x 3y = 4 where, x = 19/5, y = 6/5 , (ii) 3x 4y = 10 and 2x 2y = 2 where, x = 2, y = 1 , (iii) 3x 5y 4 = 0 and 9x = 2y 7 where, x = 9/13, y = 5/13, (iv) x/2 2y/3 = 1 and x y/3(x, y) = (35, 2) Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here Solving linear equations using substitution method Solving linear equations using cross multiplication method Solving one step equations

Dfraca1a2dfracbb2 C See How To Solve It At Qanda

70以上 X 2y 5 Y 2x 2 X 2 Y 2 5 2x Y 4 Sipjosjolali

 Substitution method 1)The system of equations are y = 4x 9 and y = x 3 Find the value of x by substituting x 3 for y in the First equation x 3 = 4x 9 3x = 6 x = 2 Substitute the x value in second equation y = 2 3 y = 1Find an answer to your question Solve, using the substitution method 4x 2y = 11 x – 2 = – 2y A B C DClick here👆to get an answer to your question ️ Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x 3y = 4 (ii) 3x 4y = 10 and 2x 2y = 2 (iii) 3x 5y 4 = 0 and 9x = 2y 7 (iv) x2 2y3 = 1 and x y3 = 3

Graph Graph Inequalities With Step By Step Math Problem Solver

Maths Class 10 Pages 51 100 Flip Pdf Download Fliphtml5

Substitution Method in Algebra!HELP PLZ!From equation (1), we can substitute for x x into equation (2) as 5(3y1)−2y =18 5 ( 3 y 1) − 2 y = 18 Expanding the lefthand side of the equation using the distributive property ofInfinite solutions (same line) with the substitution method While we won't have a parallel line or the same line to look at and conclude if it is one or the other, y= − 6x 2 16) 7x 2y= − 7 y=5x 5 18) y= x 4 3x − 4y= − 19 ) y= − 2x 8 − 7x − 6y= − 8 22) x − 2y= − 13 4x 2y= 18 24) 3x − 4y= 15 7x y=4 26) 6x

Solve By Elimination Method X Y 2 4 X 3 2y 5 Brainly In

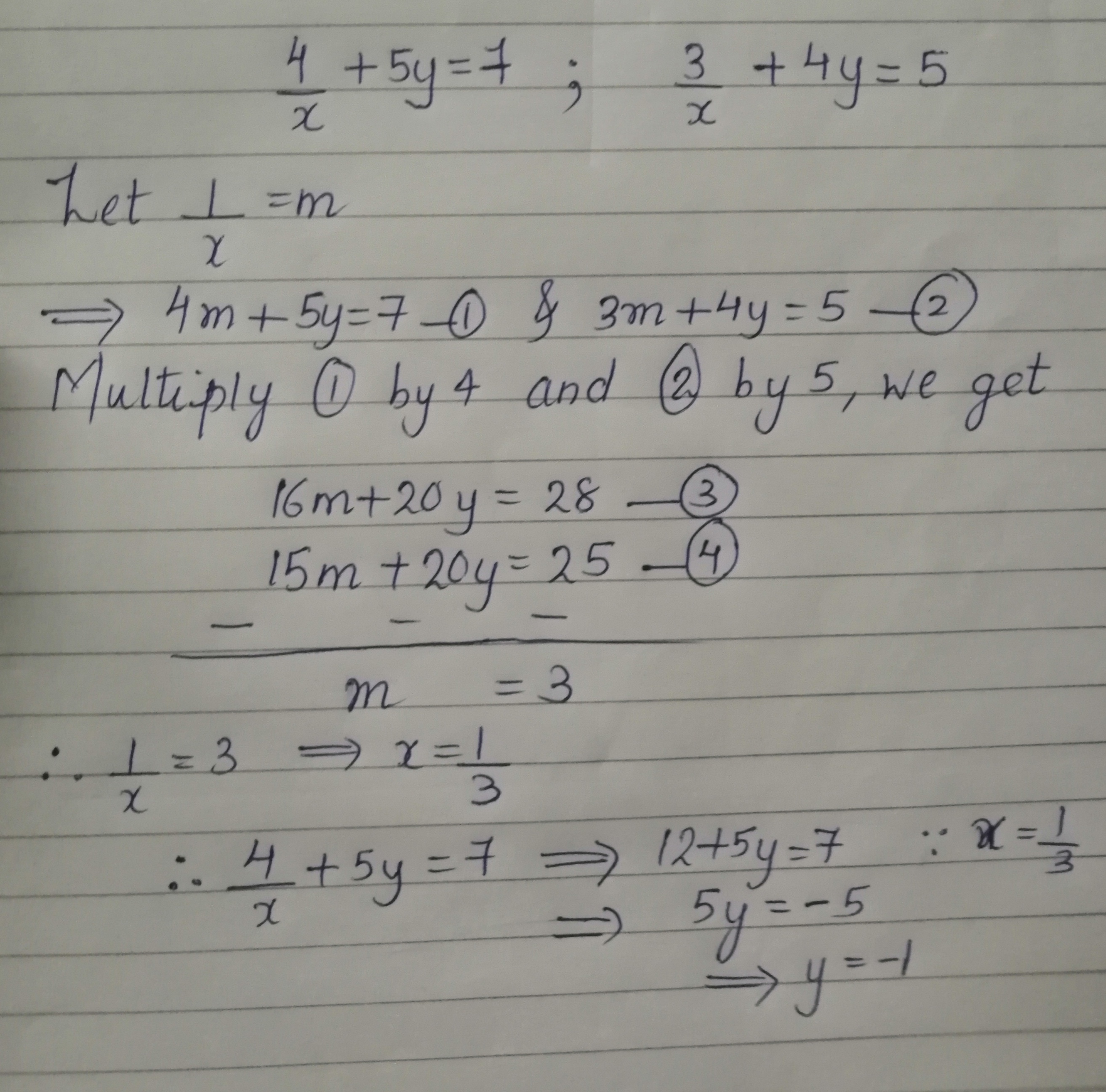
4 X 5y 7 3 X 4y 5 Mathematics Topperlearning Com Eyz2xh55

Free Substitution differential equations calculator solve differential equations using the substitution method stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more substitution\(xyyy^{2})dx(x2y)dy=0;For Solving Pair of Equation, in this Exercise Use the Method of Elimination by Equating Coefficients 3 (X 5) = Y 2 2 (X Y) = 4 3y Mathematics Advertisement Remove allMethod 1) Substitution Step 1 Rearrange to make either x ory the subject, whichever is easierEg Rearranging A) to make x the subject gives x = 2y 3 Step 2 Substitute this into the second equationSubstituting x = 2y 3 into B) gives y = 4 (2y 3) 4 Step 3 Rearrange and simplifyNeed to get all the y's on one side of the equals sign!

Maxima 5 45 0 Manual

6 3 Substitution Method Simultaneous Linear Equations Siyavula

  Solve by substitution method answer is a solution set 1) 5x4y=4 x=124y 2) 4x7=y 3xy=0 3) x=9y6 Answered by a verified Math Tutor or TeacherSolve by Substitution xy=5 , xy=1, Subtract from both sides of the equation Replace all occurrences of with in each equation Tap for more steps Replace all occurrences of in with Subtract from Solve for in the first equation Tap for more steps Put this into the second equation 3 × (2 − y) 2y = 5 6 − 3y 2y = 5 6 − 5 = y y = 1 Since x y = 2 x = 2 −y = 2 − 1 = 1 Your solution x = 1 and y = 1

Using Matrices Solve The Following System Of Equations 2x 3y 5z 11 3x 2y 4z 5 X Y 2z 3 Quora

Answered Y 4 3 1 2 12x 10y 4 3 5 2 Bartleby

 Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2In this section, we will solve systems of linear equations by the substitution method Solve the system by substitution {3 x y = 5 2 x 4 y = −10 {3 x y = 5 2 x 4 y = −10 Solution We need to solve one equation for one variable Then we Answers fast please 1) y=x−63x2y=8 Use the substitution method A) (4, −2) B) (14, 8) C) (0, −6) D) (3, −3) 2) What is the xcoordinate of the

Solve The Following Pair Of Linear Equation By Substitution Method 3x 2y 7 0 4x Y 6 0

Apnacoolschool Com

Example Solve for x and y Equation A yx = 3 y x = 3 Equation B x= y5 x = y 5 Show Solution The goal of the substitution method is to rewrite one of the equations in terms of a single variable Equation B tells us that x = y 5 x = y 5, so it makes sense to substitute y 5 y 5 into Equation A for x Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4ySubstitute x = 5 back into one of the original equations to solve for y 2x 3y = 22 2(5) 3(4) = 22 10 12 = 22 22 = 22 TRUE 3x y = 19 3(5) 4 = 19 19 = 19 TRUE Check both solutions by substituting them into each of the original equations Answer x = 5 and y = 4 The solution is (5, 4)

Solved Solve The Following Systems Of Equations By Using The Chegg Com

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

5x2y=3,x5y=4 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 5x2y=3 Choose one of the equations and solve it for x by isolating x on the left hand side of the equal signAnswer (1 of 3) I always set up systems of equations vertically so it's easier to see x y = 2 2x y = 4 You want to choose either x or y to solve for Being that the y's have opposite signs and is the easiest to eliminate, we'll solve for x first Once we Add/Subtract vertically, we get 3A math video lesson on Systems of Two Equations This video solves by substitution 4x2y=10 and xy=13 #solvebysubstitution #systemsofequations #algebra2Ev

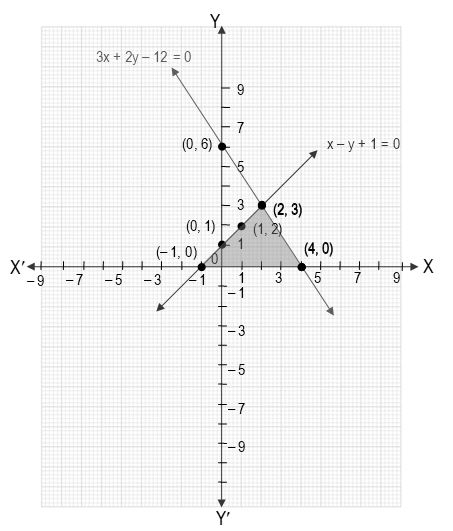
Pair Of Linear Equations In Two Variables

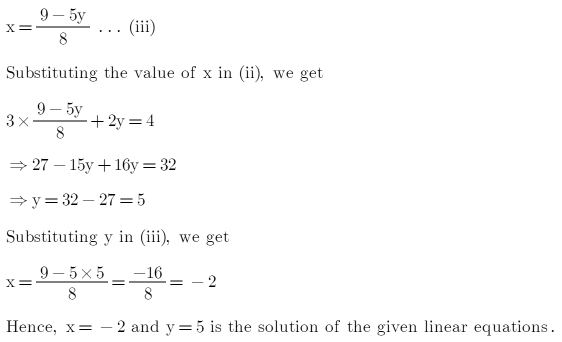
By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll

OSMBOY OSMBOY Secondary School answered X/22y/3=1 and xy/3=3 solve by elimination method 2 See answers Advertisement Advertisement KrishnaPolavarapu KrishnaPolavarapu Here's your answer Hope it was helpful Advertisement Advertisement`x y/2 = 4` (i) `x/3 2y = 5` (ii) From (i), we get `(2x y)/2 = 4` 2x y = 8 y = 8 2x From (ii), we get x 6y = 15 (iii) Substituting y = 8 2x in (iii), we get x 6(8 2x) = 15 `=> x 48 12x = 15` => 11x = 15 48 => 11x = 33 `=> x = (33)/(11) = 3` Putting x = 3 in y = 8 2x we get y = 8 2 x 3 = 8 6 = 2 y = 2Solve the following pair of linear equations by the elimination method and the substitution method Solve by matrix Method x2y3z=2 2x3yz=1 xyz=2 Solve the given pair of equations using substitution method 2xy=5,3x2y=11 Solve 2xy=5,3x2y=4 Solve 2y dy/dx=e^ ( (x^2y^2)/x) (x^2y^2)/x2x

C H A P T E R 7 Manualzz

Ppt Revision Simultaneous Equations Ii Powerpoint Presentation Free Download Id

Then substitute the result for that variable in the other equation 3x2y=12,xy=5 3 x 2 y = 1 2, x y = 5 Choose one of the equations and solve it for x by isolating x on the left hand side of the equal sign Choose one of the equations and solve it for x by isolating x The solution to the system of equations is `x=37/35, y=104/35` We are given a system of linear equations5x y = 35 x 3/2y = 34 There are a number of ways to solve a system of two linearSubstitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm144

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

Batteries Free Full Text Optimized Process Parameters For A Reproducible Distribution Of Relaxation Times Analysis Of Electrochemical Systems Html

Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4y = 12x 21y =Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0

Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook

Ncert Solutions Pair Of Linear Equations In Two Variables Class 10

We have to solve by substitution xy=2 and 3x2y=5 Solution xy=2———(i) 3x2y=5——–(ii) From equation (i)we get x = 2y Substituting the above x value in equation (ii) 3(2y) 2y = 5 6 – 3y 2y=5 6y=5y= 56y=1 y=1 So now x = 2y x=21 x=1 Answer x=1 and y=1

Solve The Simultaneous Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2

Beginner S Guide To Systems Of Equations By Brett Berry Math Hacks Medium

3 Systems Of Linear Equations

Graph Graph Inequalities With Step By Step Math Problem Solver

10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube

2

K8eh6cjfof9wlm

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

Related Videos Of Solve The Following Pairs Of Equations By Reducing Them To A Pair Of Linear Equations I 1 2x 1 3y 2 1 3x 1 2y 13 6 Ii 2 Sqrt X 3 Sqrt Y 2 4 Sqrt X 9 Sqrt Y 1 Iii 4 X 3y 14 3 X 4y 23 Iv

3 5 Solving Nonlinear Systems Ppt Download

3 Systems Of Linear Equations

7 Solve The System Of Equations Ii X 3 Y 2 X Y Homeworklib

Mathematics For Academic Studies 4 Student S Book Sample By Grupo Anaya S A Issuu

Ex 3 4 1 I Class 10 Solve By Elimination And Substitution

2

Simultaneous Equations Gmat Math Study Guide

0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question

J19

Matlab Tutorial

2

How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora

無料ダウンロード 3x 2y5 X5 Y

Get Answer X 2 Y 2 2 Transtutors

C H A P T E R 7 Manualzz

無料ダウンロード 3x 2y5 X5 Y

Solve 2x Y 5 And 3x 2y 8

Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community

The Murder Mystery Method To Solve Exact Differential

無料ダウンロード 3x 2y5 X5 Y

Solve For X And Y 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Maths Pair Of Linear Equations In Two Variables 6849 Meritnation Com

As Pure Maths Revision Notes Chemistry Part Ia Ox Studocu

Ex 3 4 1 I Class 10 Solve By Elimination And Substitution

Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations

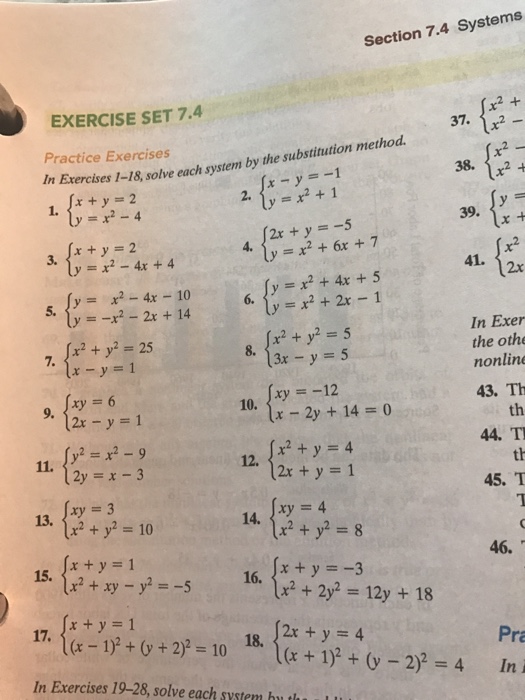
Solved Solve Each System By The Substitution Methos X Y Chegg Com

Solve X Y 7 And 3x 2y 11

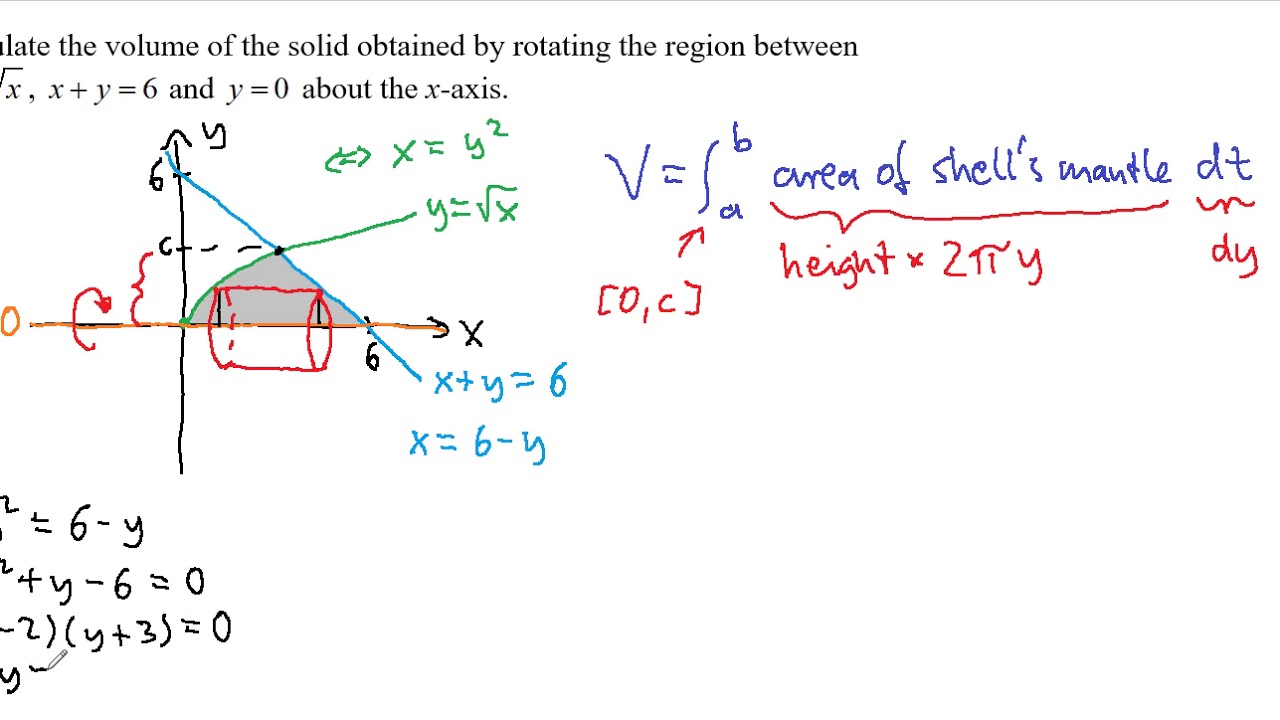
Volume Of Revolution Shell Method

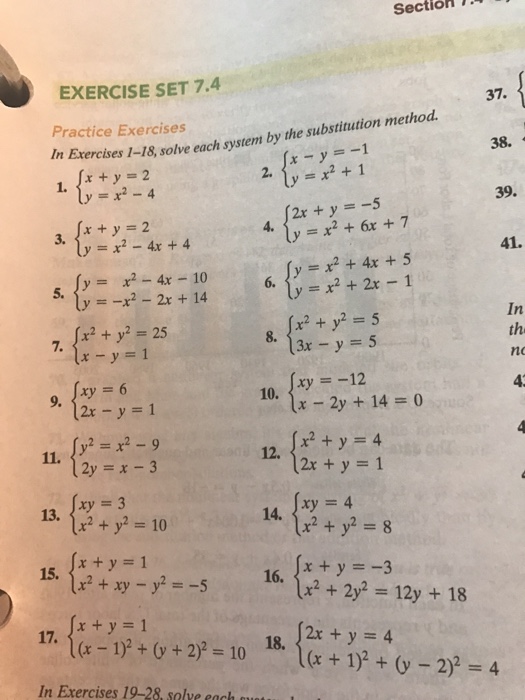
Solved Solve Each System By The Substitution Methos X Y Chegg Com

X Y 2 4 X 3 2y 5 Find It By Substitution Method Brainly In

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

Level U 2 3x 7y 10 0 Y 2x 3 0 Solde The Following Systems Of Equations 1 11x 15y 23 0 7x 2y

Solving Linear Systems By Substitution

Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy

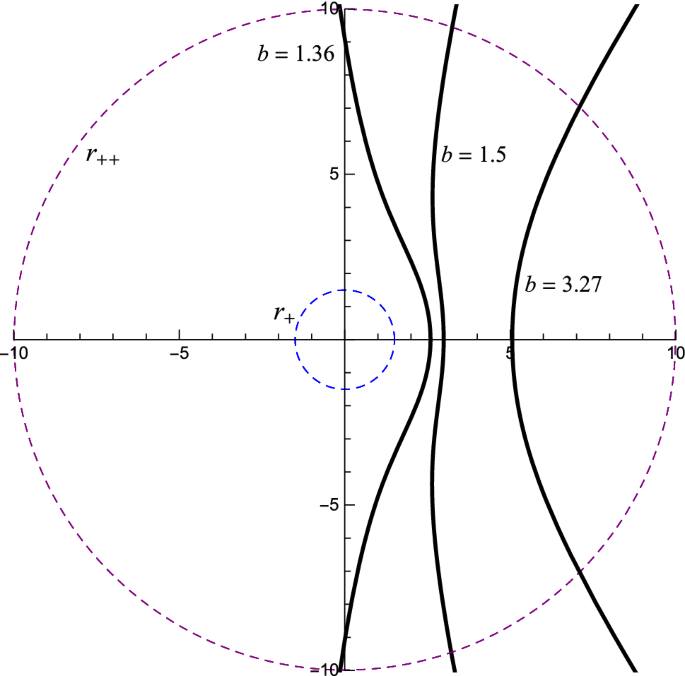
Motion Of Massive Particles Around A Charged Weyl Black Hole And The Geodetic Precession Of Orbiting Gyroscopes Springerlink

Ex 3 4 1 I Class 10 Solve By Elimination And Substitution

The Substitution Method

Ex 3 3 1 I Solve By Substitution X Y 14 X Y 4 Video

Mfm2p

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables

Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths

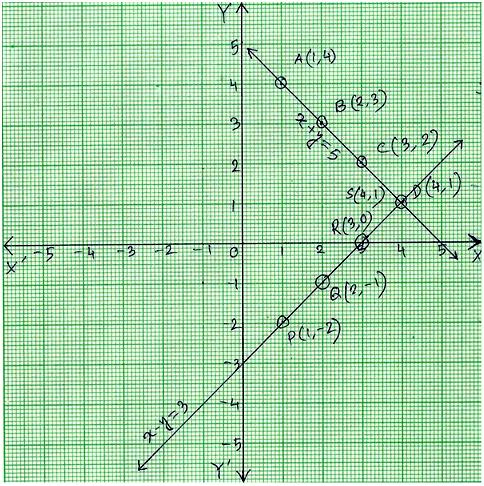
Simultaneous Equations Graphically Solve Graphically The System Of Equations

Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community

How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic

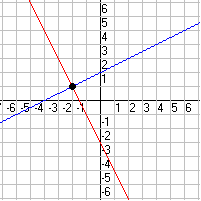
Solving Systems Of Linear Equations

Resolution De Systeme D Equations

Solved Question 01 Solve The Following Differential Equation Using Variable Separation Method 1 X4 2 X3y Sec Xy 2 2x2 3y2 7 X Dx Course Hero

X Y 2 4 And X 3 2y 5 By Substitution Method Brainly In

Solving Linear Systems With Substitution Definition Examples Expii

Systems Of Linear Equations

Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community

70以上 X 2y 5 Y 2x 2 X 2 Y 2 5 2x Y 4 Sipjosjolali

Dfraca1a2dfracbb2 C See How To Solve It At Qanda

How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora

Warm Up Solve Each Equation For X 1 Y X Y 3x 4 Ppt Download

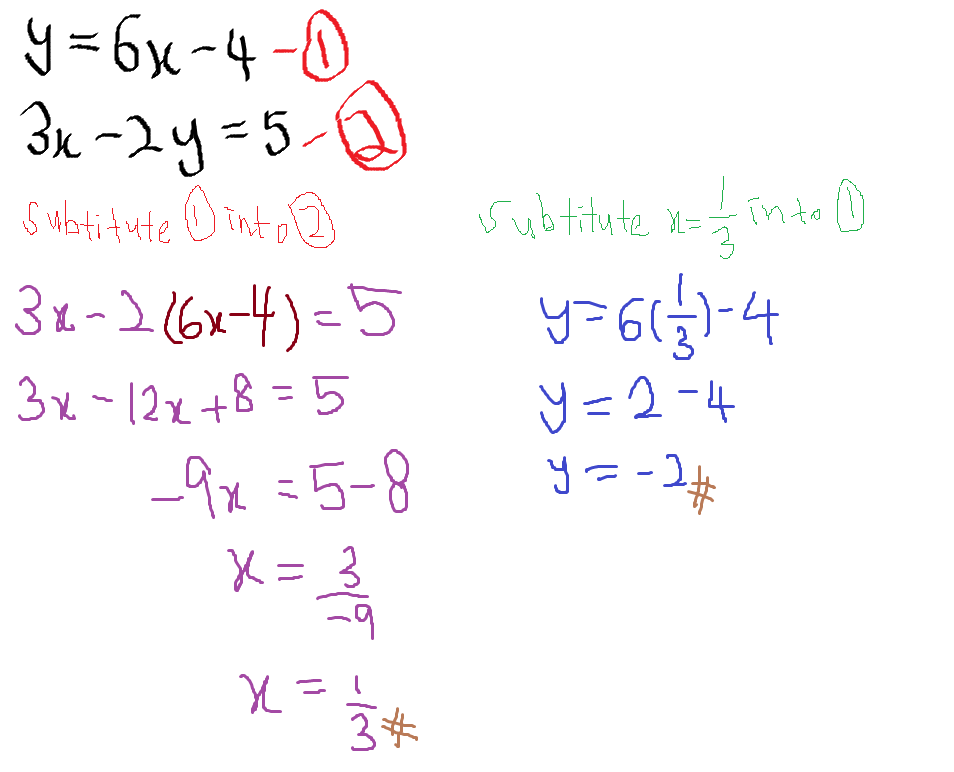
How Do You Solve Y 6x 4 And 3x 2y 5 Using Substitution Socratic

X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube

2

Pair Of Linear Equations In Two Variables Class 10 Solutions Exercise 3 3

Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables

Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu

Ideal Amino Acid Exchange Forms For Approximating Substitution Matrices Pokarowski 07 Proteins Structure Function And Bioinformatics Wiley Online Library

The Substitution Method

6 2 Presentation

2

Incoming Term: x y/2 4 x/3 2y 5 substitution method,